Kosaraju's algorithm
Kosaraju 算法
- 为了找到SCC分支,首先对图G运行DFS,计算出各顶点完成搜索的时间f;
- 然后计算图的逆图GT,对逆图也进行DFS搜索,但是这里搜索时顶点的访问次序不是按照顶点标号的大小,而是按照各顶点f值由大到小的顺序;
- 逆图DFS所得到的森林即对应连通区域。
SCC 强连通分量
Strong Connected Component
- A strongly connected component (SCC) of a directed graph is a maximal strongly connected subgraph.
there are 3 SCCs in the following graph
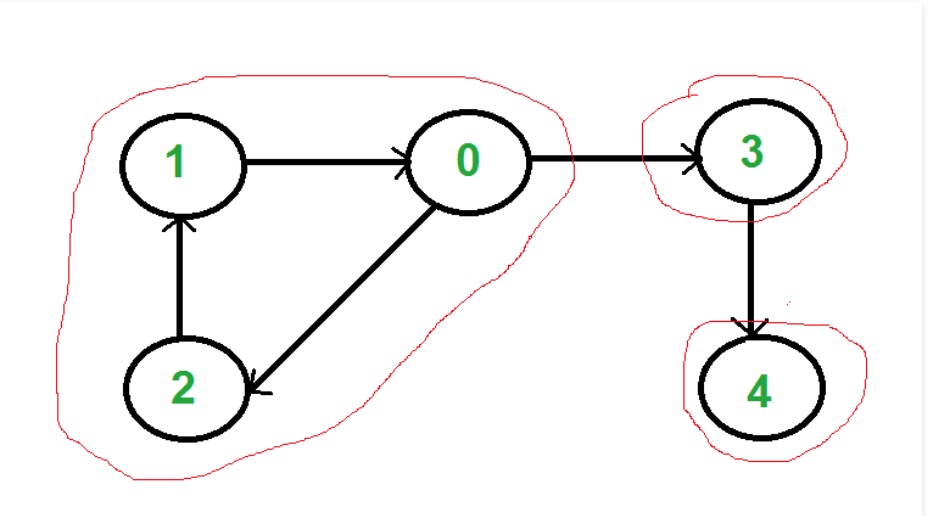
Example
We can find all strongly connected components in O(V+E) time using Kosaraju’s algorithm. Following is detailed Kosaraju’s algorithm.
- Create an empty stack ‘S’ and do DFS traversal of a graph. In DFS traversal, after calling recursive DFS for adjacent vertices of a vertex, push the vertex to stack. In the above graph, if we start DFS from vertex 0, we get vertices in stack as 1, 2, 4, 3, 0.
- Reverse directions of all arcs to obtain the transpose graph.
- One by one pop a vertex from S while S is not empty. Let the popped vertex be ‘v’. Take v as source and do DFS (call DFSUtil(v)). The DFS starting from v prints strongly connected component of v. In the above example, we process vertices in order 0, 3, 4, 2, 1 (One by one popped from stack).
How does this work?
DFS of a graph produces a single tree if all vertices are reachable from the DFS starting point. Otherwise DFS produces a forest. So DFS of a graph with only one SCC always produces a tree.
The important point to note is DFS may produce a tree or a forest when there are more than one SCCs depending upon the chosen starting point.
For example, in the above diagram, if we start DFS from vertices 0 or 1 or 2, we get a tree as output. And if we start from 3 or 4, we get a forest. To find and print all SCCs, we would want to start DFS from vertex 4 (which is a sink vertex), then move to 3 which is sink in the remaining set (set excluding 4) and finally any of the remaining vertices (0, 1, 2).
So how do we find this sequence of picking vertices as starting points of DFS? Unfortunately, there is no direct way for getting this sequence. However, if we do a DFS of graph and store vertices according to their finish times, we make sure that the finish time of a vertex that connects to other SCCs (other that its own SCC), will always be greater than finish time of vertices in the other SCC (See this for proof).
For example, in DFS of above example graph, finish time of 0 is always greater than 3 and 4 (irrespective of the sequence of vertices considered for DFS). And finish time of 3 is always greater than 4. DFS doesn’t guarantee about other vertices, for example finish times of 1 and 2 may be smaller or greater than 3 and 4 depending upon the sequence of vertices considered for DFS.
So to use this property, we do DFS traversal of complete graph and push every finished vertex to a stack. In stack, 3 always appears after 4, and 0 appear after both 3 and 4.
In the next step, we reverse the graph. Consider the graph of SCCs. In the reversed graph, the edges that connect two components are reversed. So the SCC {0, 1, 2} becomes sink and the SCC {4} becomes source. As discussed above, in stack, we always have 0 before 3 and 4.
So if we do a DFS of the reversed graph using sequence of vertices in stack, we process vertices from sink to source (in reversed graph). That is what we wanted to achieve and that is all needed to print SCCs one by one.
伪代码
- 对原图G进行深度优先遍历,记录每个节点的离开时间;
- 选择具有最晚离开时间的顶点,对反图GT进行遍历,删除能够遍历到的顶点,这些顶点构成一个强连通分量;
- 如果还没有顶点删除,继续步骤2,否则结束算法。
应用
- Oneway航班如何遍历所有的机场
- Face book好友推荐
其他视频讲解
Google 面试:机场问题
PS:评论区太搞笑了,哈哈哈哈哈哈