Dynamic Programming

Posted on In
Symbols count in article: 4.4k Reading time ≈ 4 mins.

动态规划

已知问题规模为n的前提A，求解一个未知解B。
此时，如果把问题规模降到0，即已知A0，可以得到A0->B。

  • 如果从A0添加一个元素，得到A1的变化过程，即A0->A1；进而有A1->2; A2->A3；……；Ai->Ai+1。这就是严格的归纳推理，也就是我们经常使用的数学归纳法；
  • 对于Ai+1，只需要它的上一个状态Ai即可完成整个推理过程（而不需要更前序的状态）。我们将这个模型称为马尔可夫模型，对应的推理过程叫做“贪心法”。

然而，Ai与Ai+1往往不是互为充要条件，随着i的增加，有价值的前提信息越来越少，我们无法仅仅通过上一个状态得到下一个状态，因此可以采用如下的方案：

  • {A1->A2}; {A1, A2->A3}; {A1,A2,A3->A4};……; {A1,A2,…,Ai}->Ai+1. 这种方式就是第二数学归纳法。
  • 对于Ai+1需要前面的所有前序状态才能完成推理过程。我们将这一模型称为高阶马尔科夫模型。对应的推理过程叫做“动态规划法”。

能用动态规划解决的问题的特点

能采用动态规划求解的问题的一般要具有3个性质：

  • （1）最优化原理：如果问题的最优解所包含的子问题的解也是最优的，就称该问题具有最优结构，即满足最优化原理。
  • （2）无后效性：即某阶段状态一旦确定，就不受这个状态以后的决策影响。也就是说，某状态以后的过程不会影响以前的状态，只与当前状态有关。。
  • （3）有重叠子问题：即子问题之间是不独立的，一个子问题在下一阶段决策中可能被多次使用到。
    该性质并不是动态规划使用的必要条件，但是如果没有这条性质，动态规划算法同其他算法相比就不具备优势

动态规划解题的一般思路

动态规划所处理的问题是一个多阶段决策的问题，一般由初始状态开始，通过对中间阶段决策的选择，达到结束状态。这些决策形成了一个决策序列，同时确定了完成整个过程的一条活动路线（通常是最优的活动路线）。
动态规划的设计都有着一定的模式，一般要经历以下几个步骤：

初始状态→│决策１│→│决策２│→…→│决策ｎ│→结束状态
  • 划分阶段：按照问题的时间或者空间特征，把问题分为若干个阶段。在划分阶段时，注意划分后的阶段一定要是有序的或者可排序的，否则问题就无法求解。
  • 确定状态和状态变量：将问题发展到各个阶段时所处于的各种客观情况用不同的状态表示出来。当然，状态的选择要满足无后效性。
  • 确定决策并写出状态转移方程：因为决策和状态转移有着天然的联系，状态转移就是根据上一阶段的状态和决策来导出本阶段的状态。所以如果确定了决策，状态转移方程也就可写出。但事实上常常是反过来做，根据相邻两个阶段的状态之间的关系来确定决策方法和状态转移方程。
  • 寻找边界条件：给出的状态转移方程是一个递推式，需要一个递推的终止条件或边界条件。

算法实现的步骤

  1. 创建一个一维数组或者二维数组，保存每一个子问题的结果，具体创建一维数组还是二维数组看题目而定，基本上如果题目中给出的是一个一维数组进行操作，就可以只创建一个一维数组，如果题目中给出了两个一维数组进行操作或者两种不同类型的变量值，比如背包问题中的不同物体的体积与总体积，找零钱问题中的不同面值零钱与总钱数，这样就需要创建一个二维数组。
  2. 设置数组边界值，一维数组就是设置第一个数字，二维数组就是设置第一行跟第一列的值，特别的滚动一维数组是要设置整个数组的值，然后根据后面不同的数据加进来变幻成不同的值。
  3. 找出状态转换方程，也就是说找到每个状态跟他上一个状态的关系，根据状态转化方程写出代码。
  4. 返回需要的值，一般是数组的最后一个或者二维数组的最右下角。

代码基本框架：

斐波那契数列

  • 递归

    1
    2
    3
    4
    5
    6
    7
    if(n == 0){
    	return 0;
        }else if(n == 1){
    	return 1;
        }else{
    	return solutionFibonacci(n-1)+solutionFibonacci(n-2);
        }

  • 动态规划

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    int solutionFibonacci(int n){
    		if(n==0){
    			return 0;
    		}else if(n == 1){
    			return 1;
    		}else{
    			int result[] = new int[n+1];
    			result[0] = 0;
    			result[1] = 1;
    			for(int i=2;i<=n;i++){
    				result[i] = result[i-1] + result[i-2];
    			}
    			return result[n];
    		}

数组最大不连续递增子序列

arr[] = {3,1,4,1,5,9,2,6,5}的最长递增子序列长度为4。即为：1,4,5,9

  • 设置一个数组temp，长度为原数组长度，数组第i个位置上的数字代表0…i上最长递增子序列。。当增加一个数字时，最大递增子序列可能变成前面最大的递增子序列+1，也可能就是前面最大递增子序列。
  • 这需要让新增加进来的数组arr[i]跟前面所有数字比较大小，即
    • 当 arr[i] > arr[j]，temp[i] = max{temp[j]}+1，其中，j 的取值范围为：0,1…i-1
    • 当 arr[i] < arr[j]，temp[i] = max{temp[j]}，j 的取值范围为：0,1…i-1
  • 所以在状态转换方程为$temp[i]=max{temp[i-1], temp[i-1]+1}$
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
int MaxChildArrayOrder(int a[]) {
		int n = a.size();
		int temp[] = new int[n];//temp[i]代表0...i上最长递增子序列
		for(int i=0;i<n;i++){
			temp[i] = 1;//初始值都为1
		}
		for(int i=1;i<n;i++){
			for(int j=0;j<i;j++){
				if(a[i]>a[j]&&temp[j]+1>temp[i]){
					//如果有a[i]比它前面所有的数都大，则temp[i]为它前面的比它小的数的那一个temp+1取得的最大值
					temp[i] = temp[j]+1;
				}
			}
		}
		int max = temp[0];
		//从temp数组里取出最大的值
		for(int i=1;i<n;i++){
			if(temp[i]>max){
				max = temp[i];
			}
		}
		return max;
	}

数字塔从上到下所有路径中和最大的路径

数字塔是第i行有i个数字组成，从上往下每个数字只能走到他正下方数字或者正右方数字，求数字塔从上到下所有路径中和最大的路径，如有下数字塔

3

1 5

8 4 3

2 6  7 9

6 2 3 5 1

最大路径是3-5-3-9-5，和为25。我们可以分别从从上往下看跟从下往上看两种动态规划的方式去解这个题

从上往下看：当从上往下看时，每进来新的一行，新的一行每个元素只能选择他正上方或者左左方的元素，也就是说，第一个元素只能连他上方的元素，最后一个元素只能连他左上方的元素，其他元素可以有两种选择，所以需要选择加起来更大的那一个数字，并把这个位置上的数字改成相应的路径值，具体过程如下图所示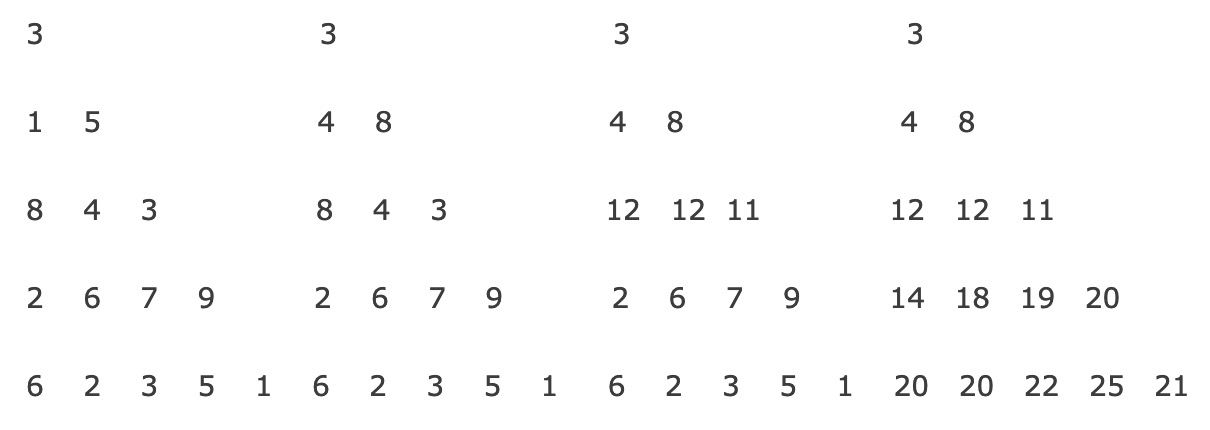

所以最大值就是最底层的最大值也就是25。
具体运算过程：

  1. 建立一个n*n的二维数组$dp[][]$，n是数字塔最后一行的数字个数，二维数组每一行数字跟数字塔每一行数字个数一样，保存的值是从上方到这一个位置最大路径的值；
  2. 填入边界值$dp[0][0]=3$；
  3. 每一行除了第一个值跟最后一个值，其他的值选择上方或者左上方更大的值与这个位置上的值相加得来的值，即$dp[i][j]=Math.max(dp[i-1][j-1], dp[i-1][j]) + n[i][j]$。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
public static int minNumberInRotateArray(int n[][]) {
		int max = 0;
		int dp[][] = new int[n.length][n.length];
		dp[0][0] = n[0][0];
		for(int i=1;i<n.length;i++){
			for(int j=0;j<=i;j++){
				if(j==0){
					//如果是第一列，直接跟他上面数字相加
					dp[i][j] = dp[i-1][j] + n[i][j];
				}else{
					//如果不是第一列，比较他上面跟上面左面数字谁大，谁大就跟谁相加，放到这个位置
					dp[i][j] = Math.max(dp[i-1][j-1], dp[i-1][j]) + n[i][j];
				}
				max = Math.max(dp[i][j], max);
			}
		}
		return max;
	}

从下往上看时：从下往上看时大体思路跟从上往下看一样，但是要简单一些，因为不用考虑边界数据，从下往上看时，每进来上面一行，上面一行每个数字有两条路径到达下面一行，所以选一条最大的就可以

具体方法也是建立一个二维数组，最下面一行数据添到二维数组最后一行，从下往上填数字，所以状态转化方程是$dp[i][j]=Math.max(dp[i+1][j+1], dp[i+1][j]) + n[i][j]$。

从下往上看跟从上往下看相比，虽然逻辑较为简单，但是从下往上看时需要得到完整的数字塔之后才能开始计算，而从上往下看时可以随着数字塔的深入来计算，也可以返回任意一层的结果，是最好的方法。

其他题目

others

动态规划和分治区别

动态规划算法：它通常用于求解具有某种最优性质的问题。在这类问题中，可能会有许多可行解。每一个解都对应于一个值，我们希望找到具有最优值的解。动态规划算法与分治法类似，其基本思想也是将待求解问题分解成若干个子问题，先求解子问题，然后从这些子问题的解得到原问题的解。与分治法不同的是，适合于用动态规划求解的问题，经分解得到子问题往往不是互相独立的。

分治法：若用分治法来解这类问题，则分解得到的子问题数目太多，有些子问题被重复计算了很多次。如果我们能够保存已解决的子问题的答案，而在需要时再找出已求得的答案，这样就可以避免大量的重复计算，节省时间。我们可以用一个表来记录所有已解的子问题的答案。

文章转载：六大算法之三：动态规划