karnaugh map
卡诺图 karnaugh map
卡诺图是由美国工程师karnaugh首先提出的一种用来描述逻辑函数的特殊方格图。
在这个方格图中,每个方格代表逻辑函数的一个最小项,而且几何相邻(在几何位置上,上下或左右相邻)的小方格具有逻辑相邻性,即两相邻小方格代表的最小项只有一个变量取值不同。
对于有n个变量的逻辑函数,其最小项有$2^n$个。
因此该逻辑函数的卡诺图又$2^n$个小方格构成,每个小方格都满足逻辑相邻项的要求。
可以运用于逻辑函数的化简。
- 例子
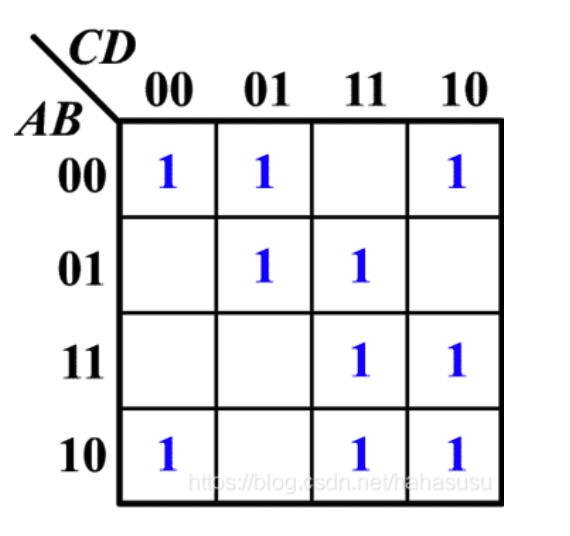
- 画出逻辑函数的卡诺图
- $F(A,B,C,D)= \sum {m(0,1,2,5,7,8,10,11,14,15)}$
应用
二灯游戏
一个游戏机有两个灯,一黄一绿,它们忽闪忽灭,你必须在出现以下情况的时候迅速按下游戏机:
- 绿灯灭,黄灯亮
- 绿灯、黄灯都灭
- 绿灯、黄灯都亮
解题思路:
- 首先定义两个基本的命题
- 命题A:绿灯亮
- 命题B:黄灯亮
- 画出卡诺图
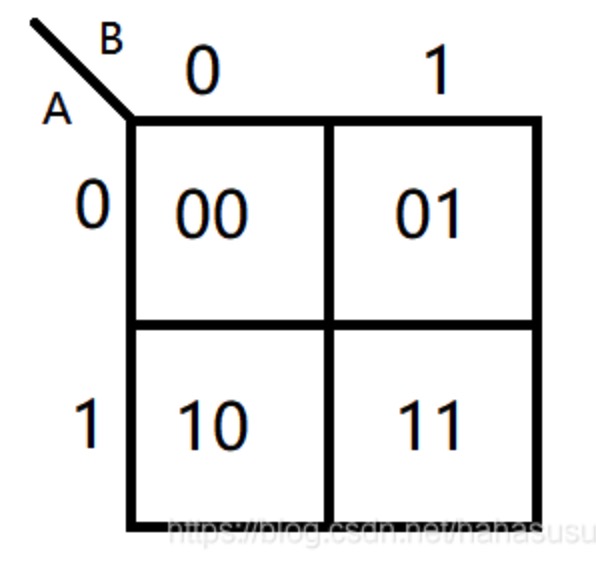
- A为绿灯,0和1分别表示该灯的状态;
- B为黄灯,同理。
根据游戏规则的3种情况,分别对应卡诺图种的:00、01、11
根据卡诺图每格具备相邻性的特点,使用11、12、22、44的网格圈出(仅能使用2^n个格子去圈)
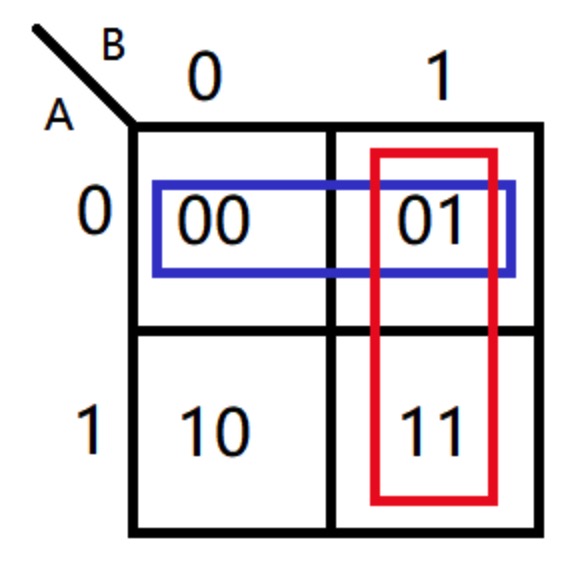
- 卡诺图化简
根据上图得出式子:(~A~B+ ~AB) + (~AB+AB)= ~A + B (~A表示A反)
由此得出只要满足 ~AV(V表示或)B ,即绿灯灭 或者 黄灯亮即可按下按钮。
三灯游戏
将上述游戏进行升级,存在3种灯(绿灯、黄灯、红灯)的情况下,符合如下规则即可按下按钮:
- 3灯都灭
- 黄灯灭、红灯亮
- 绿灯灭、黄灯亮
- 3灯都亮
解题思路:
- 定义命题
命题A:绿灯亮
命题B:黄灯亮
命题C:红灯亮 - 画出卡诺图,并将上述情况在卡诺图中用1来代替原先的二进制
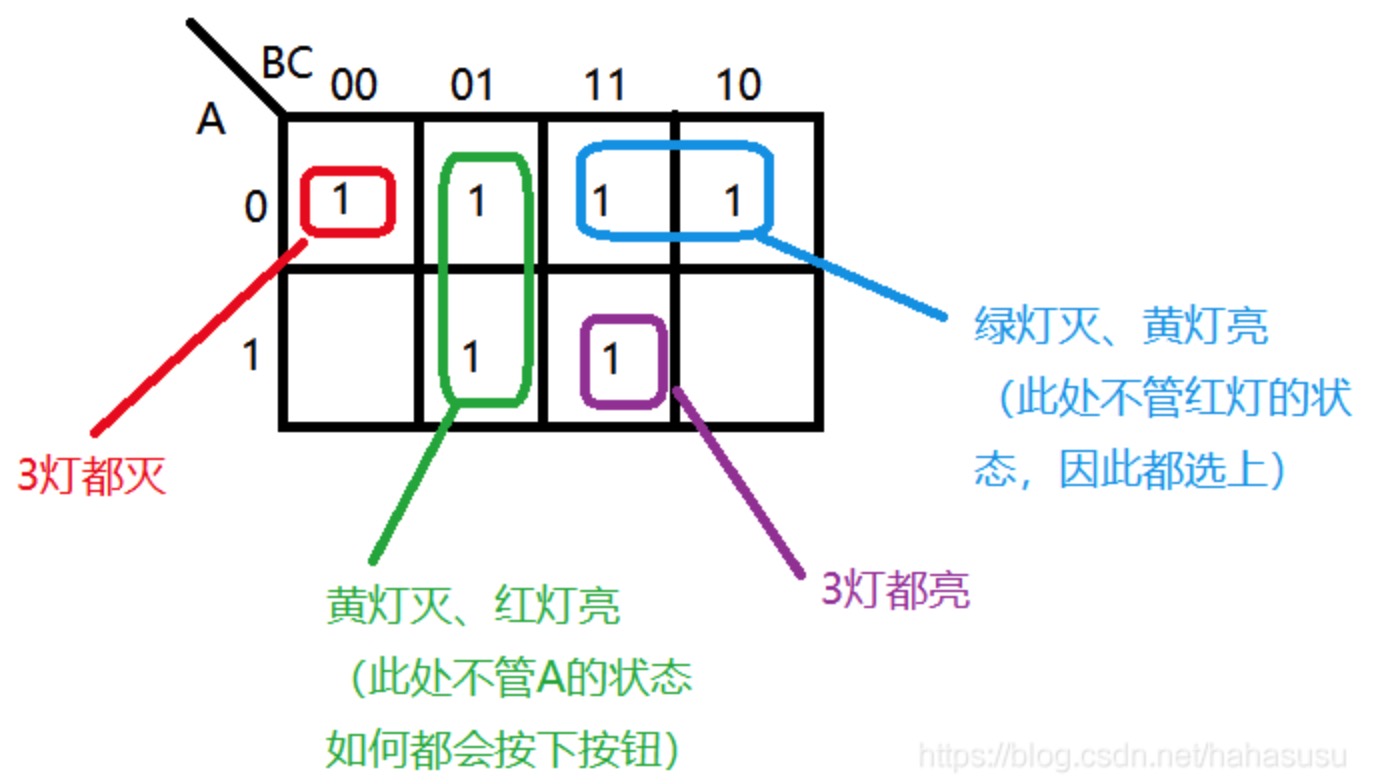
上图将4个规则在卡诺图中对应出来。
- 卡诺图化简
根据卡诺图每格具备相邻性的特点,进行如下的画圈:
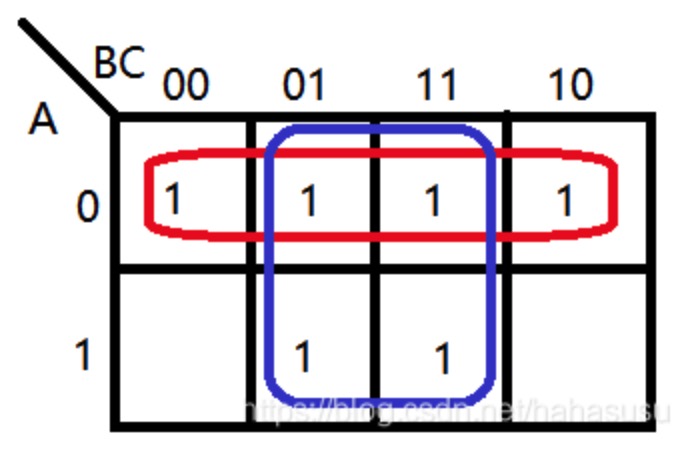
因此可得式子:(~A~B~C+A~B~C+A~BC+A~B~C) + (~A~BC+~ABC+A~BC+ABC)
= (~A~B+A~B) + (~AC+AC)
= ~A+C
化简后获得 ~A+C